Dynamics of Rotation of a Body

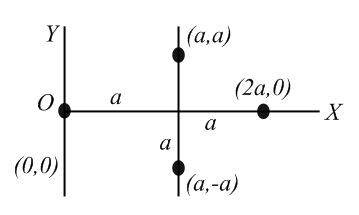
Four point masses $($each of mass $m$$)$ are arranged in the $X-Y$ plane. The moment of inertia of this array of masses about $Y$-axis is 

The dimensional formula of radius of gyration is:

In the calculation of the radius of gyration, we use intensity of loadings. So whenever the distributed loading acts perpendicular to an area its intensity varies

Point masses $1, 2, 3$ and $4 \mathrm{kg}$ are lying at the points $(0, 0, 0), (2, 0, 0), (0, 3, 0)$ and $(-2, -2, 0)$, respectively. The moment of inertia of this system about the $x$-axis will be,

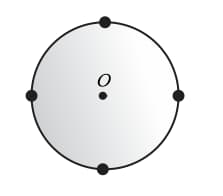
Four similar point masses (each of mass $m$) are placed on the circumference of a disk of mass $M$ and radius $R$. The moment of inertia of the system about the normal axis through the center $O$ will be,

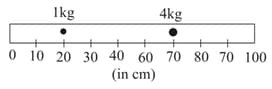
On the marks of $20 \mathrm{cm}$ and $70 \mathrm{cm}$ of a light meter scale, two weights, $1 \mathrm{kg}$ and $4 \mathrm{kg}$, respectively, are placed. The moment of inertia (in $\mathrm{kg} {\mathrm{m}}^2$) about the vertical axis through the $100 \mathrm{cm}$ mark will be,

A couple produces

The speed of a solid sphere after rolling down from rest without sliding on an inclined plane of vertical height h is

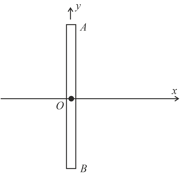
At shown instant a thin uniform rod $\mathrm{AB}$ of length $L=1 \mathrm{m}$ and mass $m=1 \mathrm{kg}$ is coincident with $y-$axis such that centre of rod is at origin. The velocity of end $A$ and centre $O$ of rod at shown instant are ${\overrightarrow{v}}_{\mathrm{A}}=-2\hat{\mathrm{i}} \mathrm{m} {\mathrm{s}}^{-1}$ and ${\overrightarrow{v}}_0=10\hat{\mathrm{i}} \mathrm{m} {\mathrm{s}}^{-1}$ respectively. Then the kinetic energy of rod at the shown instant is:

These questions consists of two statements each printed as Assertion and Reason. While answering these questions you are required to choose any one of the following five responses.

Assertion: If we draw a circle around the centre of mass of a rigid body, then moment of inertia about all parallel axes passing through this circle has a constant value.
Reason: Dimensions of radius of gyration are $\left[{\mathrm{M}}^0{\mathrm{LT}}^0\right]$

A closed cylindrical container is partially filled with water. As the container rotates in a horizontal plane about a perpendicular, its moment of inertia

The inductance in a coil plays the same role as

A uniform circular disc of mass $400 \mathrm{g}$ and radius $4.0 \mathrm{cm}$ is rotated about one of its diameter at an angular speed of $10 \mathrm{rad} {\mathrm{s}}^{-1}$. The kinetic energy of the disc is

The ring of radius $1 \mathrm{m}$ and mass $15 \mathrm{kg}$ is rotating about its diameter with angular velocity of $25\mathrm{rad}/\sec$. Its kinetic energy is

A couple produces,

The angular momentum of a particle describing uniform circular motion is $L$. If its kinetic energy is halved and angular velocity doubled, its new angular momentum is

A body having a moment of inertia about its axis of rotation equal to $3 \mathrm{kg} {\mathrm{m}}^2$ is rotating with an angular velocity of $3 \mathrm{rad} {\mathrm{s}}^{-1}$. Kinetic energy of this rotating body is same as that of a body of mass $27 \mathrm{kg}$ moving with a velocity $v$. The value of $v$ is

The rotational $KE$ of a body is $E$ and its moment of inertia is $I$. The angular momentum is

Energy of $1000 \mathrm{J}$ is spent to increase the angular speed of a wheel from $20 \mathrm{rad} {\mathrm{s}}^{-1}$ to $30 \mathrm{rad} {\mathrm{s}}^{-1}$. Moment of inertia of the wheel in $\mathrm{kg} {\mathrm{m}}^2$ 

A wheel of mass $10 \mathrm{kg}$ and radius $0.8 \mathrm{m}$ is rolling on a road with an angular speed $20{\mathrm{rads}}^{-1}$ without sliding. The moment of inertia of the wheel about the axis of rotation is $1.2{\mathrm{kgm}}^2,$ then the percentage of rotational kinetic energy in the total kinetic energy of the wheel is ____________(approximately)